Regression Function: f(x), irreducible error, reducible error, Bias, Variance
포스트 난이도: HOO_Senior
# Irreducible Error
이전 포스트에서 Regression function과 Mean-squared prediction error(MSE)에 대해서 알아보았다.
https://whoishoo.tistory.com/565
[Statistical Machine Learning] Regression Function: f(x), expected value, Mean-squared Prediction Error
Regression Function: f(x), expected value, Mean-squared Prediction Error 포스트 난이도: HOO_Senior # Ideal f(x) 저번 포스트에서 Statistical machine learning(SML)에 대해 무엇이며, 어떤 기본 공식을 가지고 있는지 알아보았
whoishoo.tistory.com
저번 포스트에서 다룬 MSE 말고도 regression function에서 고려해야 될 에러가 또 있다. irreducible error는 MSE를 통해서 에러를 예측했다 할지라도 distribuition 과정에서 발생할 수 있는 에러이다. 따라서 우리는 MSE 외에도 irreducible error를 고려해서 regression function을 구성해야 한다. irreducible error는 아래와 같이 표현이 가능하다.

Y값에 f(x)값을 빼준 것이 irreducible error에 대한 값이고 수식을 바꿔주면 Y에 irreducible error를 빼준 것이 regression function이 된다.
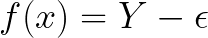
따라서 irreducible error까지 적용해 준 최종 계산식은 아래와 같이 나온다.
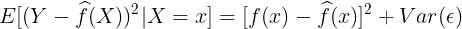
여기서 앞의 부분은 Reducible를 의미하고 뒤의 Var() 부분은 Irreducible를 의미한다. Reducible error에 대해서 조금 더 살펴보자면, Statistical machine learning에서 줄일 수 있는 에러에 해당되는 녀석들이다. 대표적으로 Bias나 Variance가 여기에 해당하는 에러들이다. 이론만 본다면 Bias와 Variance까지 알아둘 필요는 없지만 ML를 돌리는 개발자이기에 두 개의 에러가 무엇인지 알아둘 필요가 있다. 우선 이번 포스트는 SML에 대한 부분이기에 Reducible error에 대해서 간단하게만 살펴보도록 하자.
# Bias
Bias는 영단어에서 자주 보는 단어 중 하나이다. "편향" 또는 "편견" 등의 뜻을 가지고 자주 사용되고 봐왔던 단어 중에 하나이다. 단어의 뜻에 너무 집중할 필요 없지만 이해하는데 참고 정도로만 받아들이면 ML에서 Bias를 이해하는데 수월할 것이다. 우선 ML를 돌리다 보면 예측값과 실제값이 차이가 나는 건 어쩔 수 없는 일이고 빈번하게 있다. 한마디로 실제와 예측이 차이가 난다는 것이다. 우리가 ML를 돌린다는 것은 실제 우리 생활에 있는 데이터를 분석하는 것이고 현실 세계에 존재하는 데이터는 몇 가지의 원인으로 발생되지 않는다. 쉽게 말하면 마늘을 키우는 데 있어서 흙과 물만 있으면 키울 수가 없다는 것이다. 마늘이 생장하는 데 있어 영향을 끼치는 요소들이 무수히 많다. 심지어 애벌레가 마늘의 잎에 기어가는 행위조차도 마늘 생장에 영향을 아주 조금이라도 줄 수가 있다. 이렇다 보니, 실제 데이터가 영향을 받을 수 있는 경우의 수는 무수히 많다. 그렇다 보니 실제 결과와 예측 결과의 차이가 발생하고 여기서 경우의 수라는 에러도 같이 발생되는 것이다. 서론이 길었는데, Bias는 실제 결과와 예측 결과의 차이를 나타낸다. 이걸 우리는 Model predictions과 Actural values 사이에 발생되는 간극 또는 간격을 Bias라고 하며, 이것을 줄일 수 있는 에러인 Reducible error라고 한다.
너무 많은 정보를 이번 포스트에 담고자 하는 것 같아 글쓴이가 미안함을 느끼지만 Bias에 대해서 조금 더 언급하자면 underfitting 문제가 발생하는 원인이 바로 Bias이다. ML를 다루다보면 흔히 데이터 분석하는 과정에서 overfitting이 되었다 또는 underfitting이 되었다는 이야기를 들어봤을 것이다. Bias로 인해서 잘못된 일반화로 인해 예측 모델이 나타내야 하는 특성을 제대로 파악하지 못하여 ML로써 또는 SML로써 가치가 없는 데이터가 산출될 수 있다. 한마디로 훈련 모델에서 특정 패턴을 찾지 못하고 테스트 데이터를 통해서도 원하는 결과가 산출되지 않는다는 것이다. 여기서 패턴을 찾지 못한다는 결과가 바로 underfitting이 발생되었다는 것을 의미한다.
# Variance
Variance는 Bias와 같이 reduicble error이지만 반대되는 특징을 가지고 있는 에러에 해당된다. 앞선 Bias가 되게 보수적인 느낌을 가지고 있다면 Variance는 유연한 느낌을 주는 에러이다. Bias는 다양한 데이터를 분석하는데 있어서 발생할 수 있는 경우의 수들을 고려하지 못하여 학습 데이터의 유연함을 주지 못하는 반면에 Variance는 학습 데이터의 유연함을 너무 많이 줘서 제대로 된 학습이 이루어지지 못한 경우를 의미한다. Variance라는 단어 뜻을 살펴보면 "변화" 또는 "분산"이라는 의미를 가지고 있는데, 단어의 의미와 비슷하게 변화에 대해서 매우 배려심이 많은 녀석이다 보니 noise에 대해서도 학습이 이루어진다는 것이다. 예측 데이터가 가져야 할 특성 외에도 noise에서 발생한 특성까지도 포함하다 보니 실질적으로 Variance도 원하는 결과를 산출해 낼 수가 없다. 우리는 이것을 overfitting이라고 부른다. 간단한 예시를 들자면, 사람의 얼굴을 가지고 예측 모델을 만든다고 가정했을 때, overfitting이 발생할 경우에는 사람이 아닌 외계인이나 동물 또는 동상까지도 사람으로 인식해 버린다. 그렇기에 우리는 overfitting과 underfitting이 발생하지 않도록 유의하여 모델을 개발해야 하며, 이러한 reducible error를 Regression funciton에서 고려해야 한다는 것이다.

댓글