MLE with data from exponential distribution
포스트 난이도: HOO_Senior
# Example
LetX1, . . . , X100be independent rvs from the exponential distribution with rateλ(i.e., rate is thereciprocal of the population mean here). Nature uses the following code to generate the data:
set.seed(0);
x = rexp(100,10);
I.e., in the game theory setup, Nature chosesλ= 10, but this is not known to the Statistician.
# Example 1
(Computational) Use the examples from class to estimate λ using the method of maximum likelihood.Show all steps.
우선 estimate λ 를 사용해서 Maximum likelihood를 어떻게 추정하는지를 구해야 하기 때문에 우리는 Maximum likelihood estimator(MLE)를 사용할 수 있다.
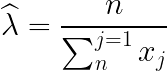
\widehat{\lambda }=\frac{n}{\sum_{n}^{j=1}x_j}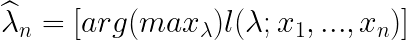
\widehat{\lambda}_n=[arg(max_\lambda ) l(\lambda ;x_1,...,x_n)]MLE를 하기 전에 최댓값에 대한 조건은 log-likelihood에 미분한 값이 0으로 수렴한다는 것이다.
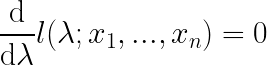
\frac{\mathrm{d} }{\mathrm{d} \lambda }l(\lambda ;x_1,...,x_n)=0
\frac{\mathrm{d} }{\mathrm{d} \lambda }l(\lambda ;x_1,...,x_n)=\frac{\mathrm{d} }{\mathrm{d} \lambda }((n)ln(\lambda )-\lambda \sum_{j=1}^{n}x_j)위의 식을 계산하면 log-likelihood function을 통해서 아래와 같이 결과가 산출된다.

\frac{n}{\lambda }-\sum_{j=1}^{n}x_j왜냐하면! log-likelihood function을 증명하면 아래와 같이 나오기 때문이다.

l(\lambda ;x_1,...,x_n)=(n)ln(\lambda )-\lambda \sum_{j=1}^{n}x_j
l(\lambda ;x_1,...,x_n)=ln(L(\lambda ;x_1,...,x_n))=ln(\lambda ^{n})+ln(exp(-\lambda \sum_{j=1}^{n}x_j))=(n)ln(\lambda )-\lambda \sum_{j=1}^{n}x_j그리고 조건에서 0과 동일하다고 했기 때문에 우리는 아래와 같은 결과를 얻을 수 있다.
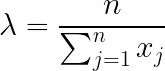
\lambda =\frac{n}{\sum_{j=1}^{n}x_j}여기서 중요한 점은 지수 분포 랜덤 변수는 양의 값만 취할 수 있기 때문에 상호 간의 sample mean은 아래와 같이 나온다. 한마디로 람다의 MLE 추정 값은 아래와 같다.

\frac{\sum_{j=1}^{n}x_j}{n}
# Example 2
(Analytical) Use calculus to obtain the (expression for) MLE of λ. Show all steps (including checkingthe second-order conditions presented in class)
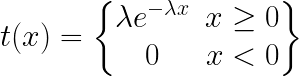
t(x)=\begin{Bmatrix}
\lambda e^{-\lambda x} & x\geq 0\\
0 & x<0
\end{Bmatrix}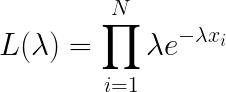
L(\lambda )=\prod_{i=1}^{N}\lambda e^{-\lambda x_i}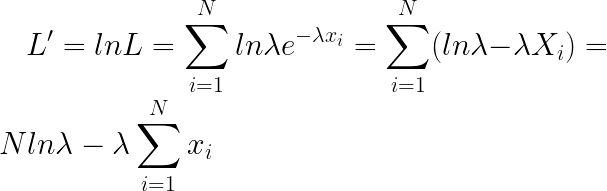
{L}'=lnL=\sum_{i=1}^{N}ln\lambda e^{-\lambda x_i}=\sum_{i=1}^{N}(ln\lambda -\lambda X_i)=Nln\lambda -\lambda \sum_{i=1}^{N}x_i
\frac{\partial \lambda{}'}{\partial \lambda }=\frac{N}{\lambda }-\sum_{i=1}^{N}X_i=0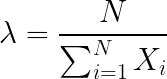
\lambda =\frac{N}{\sum_{i=1}^{N}X_i}Maximum check하면 아래와 같다.
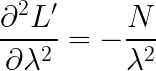
\frac{\partial ^{2}L{}'}{\partial \lambda ^{2}}=-\frac{N}{\lambda ^{2}}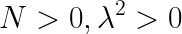
N>0, \lambda ^{2}>0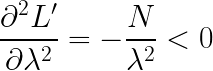
\frac{\partial ^{2}L{}'}{\partial \lambda^{2}}=-\frac{N}{\lambda ^{2}}<0
\frac{\sum_{j=1}^{n}x_j}{n}




댓글