Dijkstra's Shortest Path Algorithm
포스트 난이도: HOO_Middle
[Notice] 포스트 난이도에 대한 설명
안녕하세요, HOOAI의 Henry입니다. Bro들의 질문에 대한 내용을 우선적으로 포스팅이 되다 보니 각각의 포스트에 대한 난이도가 달라서 난이도에 대한 부분을 작성하면 좋겠다는 의견을 들었습니다
whoishoo.tistory.com
# Dijkstra Algorithm
Shortest Path를 구하는 알고리즘 중에서 대표적인 알고리즘이 Dijkstra's Shortest Path Algorithm, 또는 Dijkstra algorithm이라고 불리는 알고리즘이다. 이번 포스트에서는 Dijkstra algorithm 원리에 대해서 알아보도록 하겠다. Dijkstra algorithm에 대한 예제에 앞서서 큰 특징을 살펴보면, Prims 알고리즘과 같이 노드에 연결되어 있는 edge들을 비교해가며 최소 거리 값을 구한다. 마치 게임에서 단계별 stage를 clear 하듯이 연결되어 있는 node의 edges들을 비교하여 연결해줌으로써 최종적으로 가고자 하는 목적지에 이룰 수 있다. 이러한 특징을 기억하고 아래 Dijkstra algorithm에 대한 예제를 살펴보자.

예를 들어 위와 같은 예제가 있다고 가정해보자.
우리는 S라고 쓰여진 Start 위치부터 F라고 쓰인 Final destination까지 간다고 했을 때,
최소 거리 값을 구하기를 원한다.

처음 S의 시작 값은 0인 것을 알 수 있다.
하지만 아직 다른 노드 간의 거리값을 모르기 때문에
나머지 노드들은 거리값을 모른다는 의미에서 Infinity 표시를 해준다.

이제 S에 edge로 연결된 근접 노드들까지의 거리를 살펴보자.
각 거리 값을 다음 연결 노드 위에 작성해준다.
마찬가지로 아직 모르는 미지의 노드 거리 값에 대해서는 infinity 표시를 남겨둔다.

그다음 노드들까지의 거리 값을 더하여 다음 노드 위에 infinity 표시를 제거하고 total 거리 값을 작성한다.
여기서 유의할 점은 필자는 이해하기 쉽도록 모든 경우를 다 작성하여 표시하였다.
하지만 실제로는 그럴 필요 없이 최소 거리값만 표시하면 된다.

앞선 방법을 노드 하나씩 연결해가며 반복한다.
필자가 4번 노드에 14와 39 값을 모두 작성해준 이유는 이해를 돕기 위해서이다.
실제로는 작은 값인 14만 남겨두고 39는 지워도 된다.
실질적으로는 단거리를 구하기 위한 목적이기에 최소 값만 사용된다.
나머지 F까지의 거리값도 이와 같은 방식을 적용하면 아래와 같이 나올 것이다.

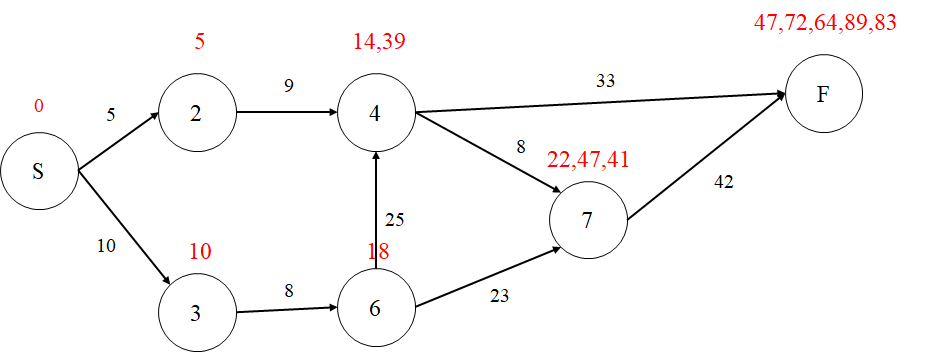
이렇게 최종 F의 거리값은 5가지가 나오지만, 실제로 할 때는 47만 나올 것이다.
결과적으로 47이 우리가 Dijkstra algorithm을 활용하여 구한 S부터 F까지의 거리 값이다.
# In conclusion, 3줄 요약
1. Dijkstra's Shortest Path Algorithm에 대해서 알아보았다.
2. 시작 Node 또는 Vertices에서 최종 목적 Node 또는 Vertices까지의 최소 값을 구한다.
3. Time Complexity는 O(E*logV)이다.
'Computer Science' 카테고리의 다른 글
| [Programming] 이분 그래프, Bipartite Graphs (0) | 2021.10.13 |
|---|---|
| [Programming] Dijkstra's Shortest Path Algorithm Concept (0) | 2021.10.09 |
| [Programming] Minimum Cost Spanning Tree(MST): Kruskals Algorithm (0) | 2021.10.06 |
| [Programming] Scrum Sprint Cycle (0) | 2021.09.29 |
| [Programming] 빅오 표기법에서 많이 사용하는 단위 정리 (Big-O Notation) (0) | 2021.09.29 |


댓글