Q: 알고리즘이 뭔가요?

알고리즘에 대해서 많이 들어보지만, 알고리즘에 대해서 명확히 모를 수 있다.
처음 컴퓨터 공학과를 가서 프로그래밍을 접한 학생의 경우 알고리즘에 대해서 이해하기 전에
수많은 프로그래밍 과제로 몸이 먼저 알고리즘에 대해서 익히게 된다.
프로그래밍에 분야에서 알고리즘에 대한 definition을 살펴보면,
문제 해결 및 결괏값 산출을 위한 단계적 절차라는 의미를 가지고 있다.
프로그래밍의 알고리즘이라고 하면 어렵게 느껴지니,
산수 과정을 통해 알고리즘에 대해 이해해보자.
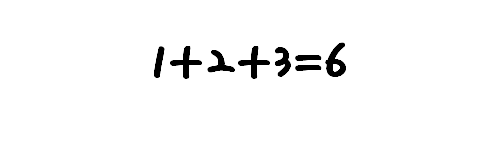
예를 들어 1+2+3=6 이라는 계산식이 있다고 가정하자.
1+2+3이라는 식을 본다면, 자연스럽게 각 숫자들을 더하여 6이라는 결괏값이 산출되는 걸 알고 있다.
초등학교 때부터 단련해온 덧셈은 눈으로만 봐도 자연스럽게 풀린다.
하지만 컴퓨터는 다르다.
1+2+3=6이라는 식의 결괏값까지 우리들은 한눈에 바로 보이지만,
컴퓨터의 경우 각각에 대한 설명이 필요하다.

숫자와 연산식에 대한 각각의 구분을 해줘야하며, 각각이 단계별 절차로써 적용된다.
1이라는 숫자 다음에 +라는 연산식이 들어가서 다음 숫자인 2와 더해지고,
또다시 +라는 연산 식이 들어가서 3이라는 숫자가 더해진다.
마지막으로 = 연산식을 통해 1+2+3이라는 결괏값은 숫자 6이 산출된다는 걸 단계적으로 처리가 된다.
사람의 경우 6이라는 결과값이 바로 보일 순 있지만, 머릿속에서는 매우 빠르게 단계별 연산처리가 이루어진다.
예를 들어, 아래와 같은 계산식이 있을 경우 1+2+3=6과 같은 즉각적인 계산이 머릿속에서 이루어지는가?

물론 산수 천재의 경우 바로 되지만, 일반적으로 1+2+3=6처럼 빠르게 결괏값이 생각나지 않는다.
왜냐하면, 계산이 복잡하기 때문에 단계적으로 더하여 결과값을 산출해야 되기 때문이다.
여기서 단계적으로 하나하나 더해가며 처리하는 것 자체가 바로 알고리즘이다.
알고리즘을 왜 사용하는가?
알고리즘이란 결과값을 산출하기 위한 Process라는 걸 알아보았다.
알고리즘을 프로그래밍에 왜 사용하는지에 대한 이유는 위의 1부터 966 더하는 계산식에서 알 수 있다.
우리가 프로그래밍을 하여 컴퓨터가 계산하게끔 만드는 이유는 컴퓨터의 계산이 정확하고 빠르기 때문이다.
복잡하고 중요한 문제일수록 미세한 실수가 용납되지 않는다.
예를 들어, 우주 로켓이나 비행선을 발사하는 과정에서 아주 미세한 수치 차이로 인해 폭발할 수 있는 가능성을 가진다.
계산 실수에 따른 발사 실패는 경제적 측면에서의 손해도 있지만
전문적으로 오랫동안 훈련해온 우주 비행사는 비행선 발사와 동시에 죽고 만다.
컴퓨터의 경우 사람이 할 수 있는 계산 실수를 하지 않는다.
다만, 정확한 알고리즘을 제공하여 올바른 결괏값 산출이 되도록 하는 것은 개발자의 몫이기에
그만큼 알고리즘이 중요하며, 알고리즘이 곧 프로그래밍이며 프로그래밍이 곧 알고리즘인 셈이다.
알고리즘은 효율성을 중시한다.
코딩을 한다는 것은 사실 누구나 할 수 있다.
3살 애기, 초등학생, 컴공과 신입생, 시니어 개발자 등에게 같은 프로그램을 만들라고 한다면 전부 만들 수 있다.
다만 누가 얼마나 빠르고 효율적으로 프로그램을 만들지는 달라진다.
프로그래밍에서 중요한 건 얼마나 효율적인 알고리즘을 구성하는지이다.
효율적인 알고리즘을 구성할수록 문제 처리 속도는 정확하고 신속히 이루어진다.
같은 프로그램일지라도 24시간이 걸려 결과가 산출되는 프로그램이 있다면,
1시간 안에 결과가 산출되는 프로그램이 있다.
이 두 프로그램의 차이는 알고리즘이 구성의 차이에서 나타난다.
결국 프로그래머는 효율적인 알고리즘을 구현할 수 있을 때 능력을 인정받는다.
'미국 개발자' 카테고리의 다른 글
| [HOO's Q&A] 코딩이 막혔을때 어떻게 해야 할까요? (0) | 2021.03.16 |
|---|---|
| [HOO's Q&A] 개발자 수습기간은 뭔가요? (0) | 2021.03.10 |
| [HOO's Q&A] 토목공학과/건축공학과인데 IoT를 배워야 할까요? (0) | 2021.02.26 |
| [HOO's Q&A] 코딩을 배워두면 좋을까요? (0) | 2021.02.24 |
| [HOO's Q&A] 3년차 프로그래머 이력서 쓰는 방법 - 분야의 정확성 (0) | 2021.02.21 |



댓글